Chapter 2: Initial Value Problems

Overview

This chapter covers numerical methods for solving initial value problems (IVPs) in ordinary differential equations.

Learning Objectives

• Understand the structure of initial value problems
• Implement explicit and implicit time integration schemes
• Analyze stability and accuracy of numerical methods

Introduction to IVPs

2.1 Definition

Initial value problems involve finding a function that satisfies a differential equation and meets specified initial conditions. The general form of an IVP is given by: \[ \dot{\underline q} \left ( t \right ) = f \left ( t, \underline q \left ( t \right )\right ), \quad t > t _ 0, \tag{1}\] where,

• \(t\) is the independent variable (often time),

• \(\underline q\) is the dependent variable (state vector, e.g., position, velocity, etc.),

  \(\forall t \ge t _ 0\), \(\underline q \left ( t \right ) \in \mathbb{R} ^ n\),

• \(f\) is a given function defining the system dynamics (model),

  \(\forall t \ge t _ 0\), \(\underline q \in \mathbb R ^ n\), \(f \left ( t, \underline q \right ) \in \mathbb{R} ^ n\).

The definition of \(q\) is completed by specifying the initial condition at time \(t _ 0\): \[ \underline q \left ( t _ 0 \right ) = \underline{q _ 0}. \tag{2}\]

NoteGlobal Cauchy–Lipschitz theorem

Let \(I = \left [ t _ a, t _ b \right ] \subset \mathbb R\) be a closed interval with \(t _ 0 \in I\). Let \(f : I \times \mathbb R ^ n \to \mathbb R ^ n\) satisfy:

1. Continuity in time and state: \(f\) is continuous on \(I \times \mathbb R ^ n\).
2. Global Lipschitz in the state (uniform in time): there exists \(L > 0\) such that for all \(t \in I\) and all \(\underline{q _ 1}\), \(\underline{q _ 2} \in \mathbb R ^ n\), \[ \left \Vert f \left ( t, \underline{q _ 1} \right ) - f \left ( t, \underline{q _ 2} \right ) \right \Vert \le L \left \Vert \underline{q _ 1} - \underline{q _ 2} \right \Vert. \]

Then the initial value problem (equations 1 and 2) admits a unique solution \(\underline q \in \mathcal C ^ 1 \left (I; \mathbb R ^ n \right )\)¹ on the whole interval \(I\).

2.2 Examples of IVPs

Radioactive decay

A simple example of an IVP is the radioactive decay of a substance, described by the equation: \[ \dot{N} \left ( t \right ) = -\lambda N \left ( t \right ), \quad N \left ( 0 \right ) = N _ 0, \tag{3}\] where \(N \left ( t \right )\) is the quantity of the substance at time \(t\), \(\lambda\) is the decay constant, and \(N _ 0\) is the initial quantity.

This is one example of a scalar (\(n = 1\)) IVP. The analytical solution is given by: \[ N \left ( t \right ) = \exp \left ( -\lambda t \right ) N _ 0. \]

The decay constant may be related to the half-life \(t _ {1 / 2}\) (the time required for half of the substance to decay) of the substance by the formula: \[ t _ {1 / 2} = \frac{\ln \left ( 2 \right )}{\lambda}. \]

Note

Equation 3 is a first-order, linear, scalar, homogeneous and autonomous IVP. It is a very valuable model that will be used throughout this course to illustrate the properties of numerical methods for IVPs.

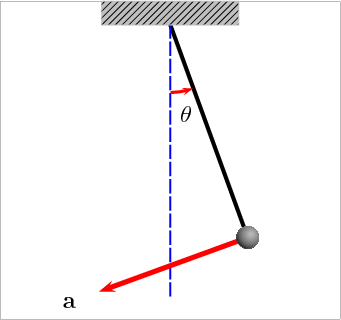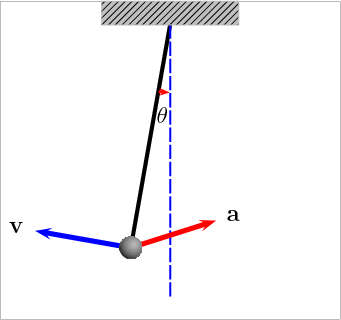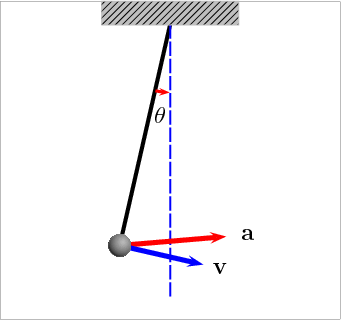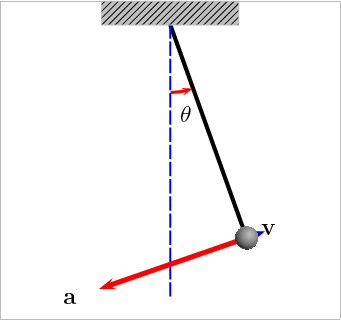
Simple pendulum

Another example of an IVP is the motion of a simple pendulum, which consists of a mass attached to a string swinging under the influence of gravity. If the friction is neglected, the total energy of the system is conserved, so one can derive a ordinary differential equation for the angle of displacement \(\theta \left ( t \right )\) from the vertical position.

The kinetic and potential energies of the pendulum are given by, \[ E _ k = \frac{1}{2} m R ^ 2 \dot \theta ^ 2, \quad \mathrm{and} \quad E _ p = -m g R \cos \theta, \] respectively. Differentiating the total energy \(E = E _ k + E _ p\) with respect to time and setting the derivative to zero (since energy is conserved) leads to, \[ m R ^ 2 \dot \theta \left ( \ddot \theta + \frac{g}{R} \sin \theta \right ) = 0. \] The first solution (\(\dot \theta = 0\)) corresponds to the trivial case of a stationary pendulum, while the second solution gives the equation of motion, \[ \ddot \theta + \omega ^ 2 \sin \theta = 0 \tag{4}\] where \(\omega = \sqrt{g / R}\).

Simple pendulum (source: Wikipedia)

Note

Equation 4 is a second-order ordinary differential equation. In order to recover the canonical form (Equation 1), we introduce the state vector \[ \underline q = \begin{bmatrix} \theta \\ \dot \theta \end{bmatrix} \] leading to the system, \[ \frac{\mathrm d}{\mathrm d t} \begin{bmatrix} q _ 1 \\ q _ 2 \end{bmatrix} = \begin{bmatrix} q _ 2 \\ - \omega ^ 2 \sin q _ 1 \end{bmatrix}. \]

2.2 Euler Methods

2.3 Runge-Kutta Methods

2.4 Multi-step Methods

2.5 Stability Analysis

Footnotes

1. Space of all functions once continuously differentiable on \(I\).